Glimpse of Auto-correction Hamming Code
Miscellaneous coding practice.
The essence of coding is math.
Guidance
For freshman, go through all sections in order.For program-orientated, skip to source code.
For a quick review, refer to flow chart.
Hint: Content is availabe by click on the last icon in the side-tab of this page.
Process-illustrative
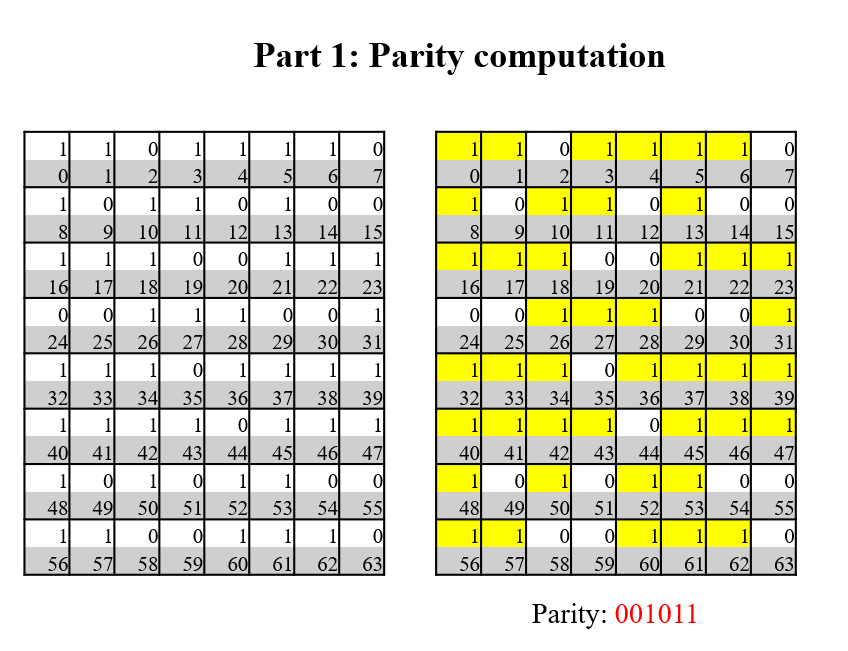
This part will combine source code in background and the input in a more interactive and illustrative way hopefully.Bits generated and parity computation
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
# generate bits for this experiment import numpy as np bits = np.random.randint(0, 2, 64) print('\n Generated bits list is: ', bits) ‘’‘==========Running=============’‘’ Generated bits list is: [1 1 0 1 1 1 1 0 1 0 1 1 0 1 0 0 1 1 1 0 0 1 1 1 0 0 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 0 1 1 1 1 0 1 0 1 1 0 0 1 1 0 0 1 1 0 0] # check the position of 1s pst = list(i for i, bit in enumerate(bits) if bit) print('\n Position of 1s are',pst) ‘’‘==========Running=============’‘’ Position of 1s are [0, 1, 3, 4, 5, 6, 8, 10, 11, 13, 16, 17, 18, 21, 22, 23, 26, 27, 28, 29, 30, 31, 32, 33, 34, 36, 37, 38, 39, 40, 41, 42, 43, 45, 46, 47, 48, 50, 52, 53, 56, 57, 60, 61] Original parity of bits is: 0b1011 |
|
1 2 |
# the single-line code for parity computation reduce(lambda x,y:x^y, [i for i, bit in enumerate(bits) if bit] |
Initializing parity
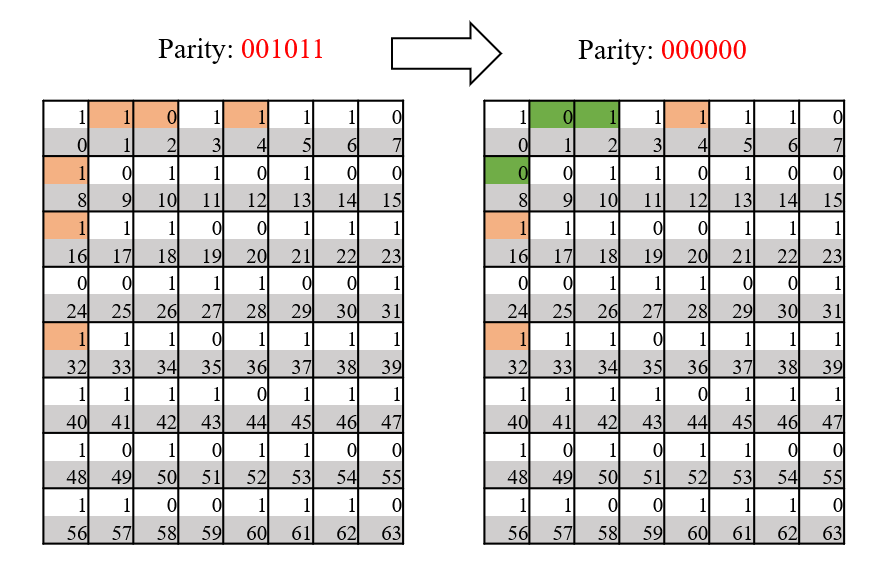
It is a trick here to initialize some togglable bit, aka redundancy, to set the parity to ‘0’. This can greatly simplify the detection of error in next step.Here the redundancy bits are somehow similar to eigenvectors, as shown by there Binary form. They are located in the orange highlighted blocks.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 |
# Toggling the parity of bits to 000000 from functools import reduce ori_par = reduce(lambda x,y:x^y, pst) # 'lambda x,y:x^y' == 'bit_1^bit_2^bit_3^...bit_n' print('\n Original parity of bits is:', bin(ori_par)) print('\n','='*10) print('\n Input Position to toggle, input 0 to exit') while 1: tg = int(input('Toggle:')) if tg == 0: print('\n Current parity:', bin(reduce(lambda x,y:x^y, [i for i, bit in enumerate(bits) if bit ]))) break else: bits[tg] = not bits[tg] print('\n Binary form of toggled position is:', bin(tg)) ‘’‘==========Running=============’‘’ Input Position to toggle, input 0 to exit Toggle:1 Binary form of toggled position is: 0b1 Toggle:2 Binary form of toggled position is: 0b10 Toggle:8 Binary form of toggled position is: 0b1000 Toggle:0 Current parity: 0b0 |
Error introduce and detect
This is the simplest part, with initialized parity. Any unary noise introduced to the series of bits will lead to change of parity. The new parity is exactly the position of the noise. Shown by code and graph.|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
# introduce noise print('\n','='*10) noise = int(input('Toggle a position as noise: ')) bits[noise] = not bits[noise] print('\n','*'*10) print('\n','*'*8) print('\n','*'*6) ns_pst = reduce(lambda x,y:x^y, [i for i, bit in enumerate(bits) if bit]) print('\n Noise is in position:', ns_pst) print('\n Binary form:', bin(ns_pst)) ‘’‘==========Running=============’‘’ Toggle a position as noise: 34 ********** ******** ****** Noise is in position: 34 Binary form: 0b100010 |
Process-lite
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 |
Generated bits list is: [1 1 0 1 1 1 1 0 1 0 1 1 0 1 0 0 1 1 1 0 0 1 1 1 0 0 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 0 1 1 1 1 0 1 0 1 1 0 0 1 1 0 0 1 1 0 0] Position of 1s are [0, 1, 3, 4, 5, 6, 8, 10, 11, 13, 16, 17, 18, 21, 22, 23, 26, 27, 28, 29, 30, 31, 32, 33, 34, 36, 37, 38, 39, 40, 41, 42, 43, 45, 46, 47, 48, 50, 52, 53, 56, 57, 60, 61] Original parity of bits is: 0b1011 ========== Input Position to toggle, input 0 to exit Toggle:1 Binary form of toggled position is: 0b1 Toggle:2 Binary form of toggled position is: 0b10 Toggle:8 Binary form of toggled position is: 0b1000 Toggle:0 Current parity: 0b0 ========== Toggle a position as noise: 34 ********** ******** ****** Noise is in position: 34 Binary form: 0b100010 |
Source Code
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 |
''' Hamming code -ref = https://www.youtube.com/watch?v=b3NxrZOu_CE An 8*8 expanded version ''' # generate bits for this experiment import numpy as np bits = np.random.randint(0, 2, 64) print('\n Generated bits list is: ', bits) # check the position of 1s pst = list(i for i, bit in enumerate(bits) if bit) print('\n Position of 1s are',pst) # Toggling the parity of bits to 000000 from functools import reduce ori_par = reduce(lambda x,y:x^y, pst) # 'lambda x,y:x^y' == 'bit_1^bit_2^bit_3^...bit_n' print('\n Original parity of bits is:', bin(ori_par)) print('\n','='*10) print('\n Input Position to toggle, input 0 to exit') while 1: tg = int(input('Toggle:')) if tg == 0: print('\n Current parity:', bin(reduce(lambda x,y:x^y, [i for i, bit in enumerate(bits) if bit ]))) break else: bits[tg] = not bits[tg] print('\n Binary form of toggled position is:', bin(tg)) # introduce noise print('\n','='*10) noise = int(input('Toggle a position as noise: ')) bits[noise] = not bits[noise] print('\n','*'*10) print('\n','*'*8) print('\n','*'*6) ns_pst = reduce(lambda x,y:x^y, [i for i, bit in enumerate(bits) if bit]) print('\n Noise is in position:', ns_pst) print('\n Binary form:', bin(ns_pst)) |
Flow Chart
Present the holistic process in a graphic approach. Good for a quick review or those who already knows the idea.
Acknowledgement
The blog is inspired by 3Blue1Brown, great thanks to this channel for showing me marvelous math theories.https://www.youtube.com/watch?v=b3NxrZOu_CE
And a note for myself:
Next time, do these stuff at night.