ODEs&Chaos

齐次微分方程与混沌理论

[latexpage]

Basics

Integral curves

If an ODE $\frac{dy}{dx}=f(x,y)$ has solution $y=\phi(x)$ We call curve $y=\phi(x)$ the integral curve.

An example for equation labeling and referring

\begin{equation}
\(\frac{dy}{dx}\)\label{eq:1}
\end{equation}
as mentioned in \ref{eq:1}

Textbook for ODE learning

Find this website of the book {Introduction to Differential Equations}
Currently following the impulse differential equations and laplace transform {Link}

A 1-D balldrop simulator for fun

\begin{align}
\frac{d^2 y}{dt^2} &= -mg\\
\frac{d^2 y}{dt^2} &= -g \\
\frac{dv}{dt} &= -g \\
v(t) &= v_0 – gt \\
y(t) &= y_0 + v_0 t – \frac{1}{2}gt^2 \\
\end{align}

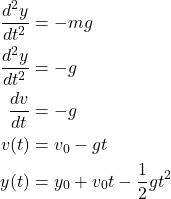
Shifts into Collision Phase
\begin{equation}
v_{\text{after}} = -e \cdot v_{\text{before}}
\end{equation}