Intriguing hypothesis in Geo 2D strain deduction
Discrepency found between Rock Mechanics Lecture notes and the book "Fundamental of Rock Mechanics"
If the formula render fails, please skip to deduction part.
Observation
On Rock Mechanic lesson,
lecture notes shows the strain in x direction as:
![\epsilon_x = \frac{1}{2}[2 \frac{\partial{u}}{\partial{x}}+ (\frac{\partial{u}}{\partial{x}})^{2}+(\frac{\partial{v}}{\partial{x}}^{2})]](https://seaofdirac.top/wp-content/ql-cache/quicklatex.com-32defde9a2560bc3ee5fd62ee02514a7_l3.png "Rendered by QuickLaTeX.com")
But the book "Fundamental of Rock Mechanics" gives strain as （Page 48 Eq. 2.180）:
Explanation
The discrepency on second-order partial derivatives is caused by 2 import hypothesis/simplification:
- Hight-order infinitesimal elements are negligible
- The approximation below: (Can verify it with L’Hospital’s Rule)
Deduction
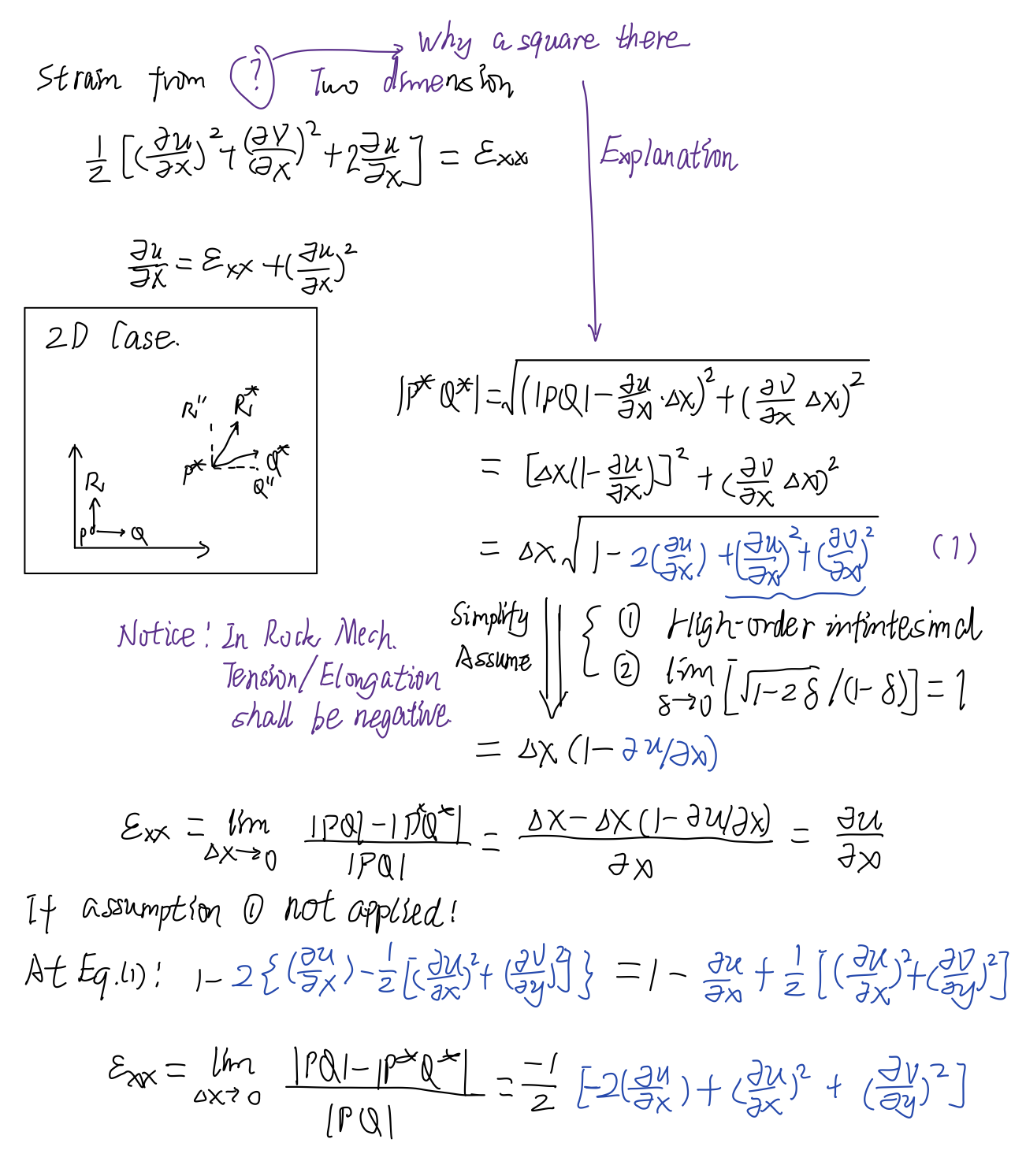
Discussion
In the book _"Fundamental of Rock Mechanics", the elongation of PQ has negative value to be consistent with the conventional compression-negative sign system in geotechnical engineering. My deduction follow the same rule. This sign definition issue worth more attention in coding and interpretation. Most code are developed on Elastic Mechanics sign system, where positive is for tensile.